JavaScript でヒートマップ写像関数

(2017-03-20更新。tumblrより記事移植。)

プログラムでヒートマップを作ろうとするたび、データと色の対応に悩むので、使いまわしのきく関数をJavascriptで書いてみた。

// HeatMap Object
//   HeatMap(_colorSet,_NaNColor,_uFlowColor,_oFlowColor)
// Properties
//   HeatMap.colorSet : Array of [r,g,b]
//   HeatMap.NaNcolor : [r,g,b]
//   HeatMap.uFlowColor : [r,g,b]
//   HeatMap.oFlowColor : [r,g,b]
// Methods
//   HeatMap.map(x) : 0<=x<=1
//   HeatMap.map(x).rgb return [r,g,b]
//   HeatMap.map(x).hex return "#rrggbb"

var HeatMap = function(_colorSet,_NaNColor,_uFlowColor,_oFlowColor){
	var rgb = function(_hex){
		var color;
			if(_hex.slice(0,1)==="#"){
				var r = parseInt(_hex.slice(1, 3), 16);
				var g = parseInt(_hex.slice(3, 5), 16);
				var b = parseInt(_hex.slice(5, 7), 16);
				color=[r,g,b];
			}else if(_hex.length==3){
				color=_hex;
			}else{
				throw new Error("Not hex or rgbArray");
			}
		return color
	}
	this.colorSet = _colorSet===undefined ? [[0,0,0],[0,0,255],[0,255,255],[0,255,0],[255,255,0],[255,0,0]] : _colorSet.map(rgb);
	this.NaNcolor = _NaNColor===undefined ? [255,255,255] : rgb(_NaNColor);
	this.uFlowColor = _uFlowColor===undefined ? this.colorSet[0] : rgb(_uFlowColor);
	this.oFlowColor = _oFlowColor===undefined ? this.colorSet[this.colorSet.length-1] : rgb(_oFlowColor);
	this.map = function(x){
		var cs=this.colorSet;
		var nc=this.NaNcolor;
		var uc=this.uFlowColor;
		var oc=this.oFlowColor;
		var c = [];
		if(isNaN(x)){
			c=nc;
		}else if(x<0){
			c=uc;
		}else if(1<x){
			c=oc;
		}else if(x==1){
			c=cs[cs.length-1];
		}else{
			var n = cs.length-1; //区分数
			var s = Math.floor(x*n); //xの区分の左端
			for (var j=0; j<3; j++){
				var y1 = cs[s+1][j];
				var y0 = cs[s][j];
				var x1 = (s+1)/n;
				var x0 = s/n;
				c[j]=Math.floor((y1-y0)/(x1-x0)*(x-x0)+y0);
				if(255<c[j]) throw new Error("c over 255");
			}
		}
		var hex = "#";
		hex+=("0"+c[0].toString(16)).slice(-2);
		hex+=("0"+c[1].toString(16)).slice(-2);
		hex+=("0"+c[2].toString(16)).slice(-2);
		return {rgb: c, hex: hex}
	}
}Code language: JavaScript (javascript)

配色パターンを好きに変えられるように、配列で等分割点の色データを与えれば間は線形補間して計算する方式にした。線形補完とか、接続点での不連続性が目立つんじゃないだろうかとも思ったが、色としてみると案外分からない。

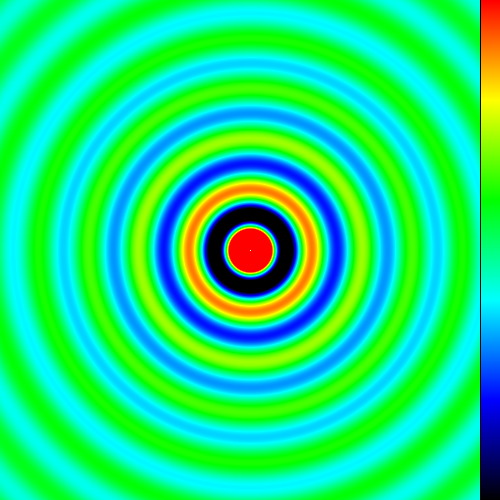
画像はサンプルで左から0~1に対応する。一つ目はよくあるパターンでBK,B,C,G,Y,Rと6分割で並ぶ。上の関数でも引数を省略するとこのパターンを用いるようにしてある。

二つ目はgnuplotのpm3dでヒートマップを描かせた時のデフォルトを模したものでgnuplot使いとしては馴染みのある配色。gnuplotでは多分グラフのような二次式が写像関数になっていると思われる。画像はこの二次式から5点を取った線形補間で作成。 

なんか違うので画像からスポイトでRGB値を調べると少し関数が違った。青が比較的キツイカーブを描くので少ないサンプルでは線形補間が変になる。カラーバーは上から４,12,20点で補間。

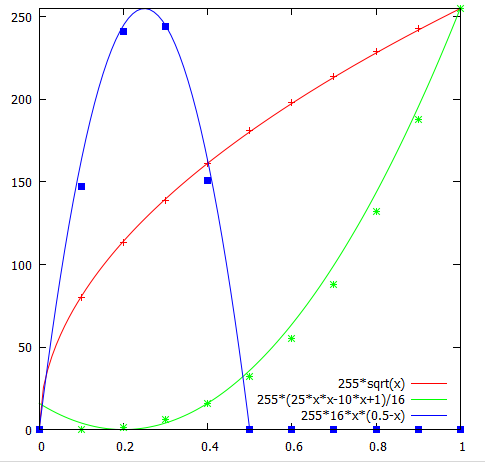
補間点の配列は以下の通り。

# 4+1 points
[[0,0,0],[128,1,255],[180,36,0],[221,121,0],[255,255,0]];
# 12+1 points
[[0,0,0],[74,0,142],[104,0,227],[128,1,255],[147,7,227],[165,19,142],[180,36,0],[195,59,0],[208,87,0],[221,121,0],[233,160,0],[244,205,0],[255,255,0]];
# 20+1 points
[[0,0,0],[57,0,92],[81,0,163],[99,0,214],[114,0,245],[128,1,255],[140,4,245],[151,9,214],[161,16,163],[171,25,92],[180,36,0],[189,49,0],[198,64,0],[206,81,0],[213,100,0],[221,121,0],[228,143,0],[235,168,0],[242,195,0],[249,224,0],[255,255,0]]Code language: CSS (css)

青のピークが1/4にあるので4の倍数で分割するのが好ましい。２０点ともなるとオリジナルと大差なくなる。

これを使って二次元ヒートマッププロッターを作ってみた。最後の画像はそれでsinc関数を描いたもの。jsファイル直リンもそちらのほうに貼ってある。